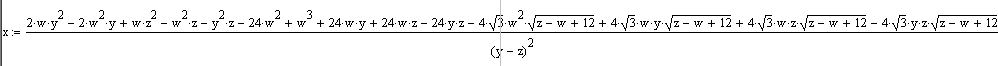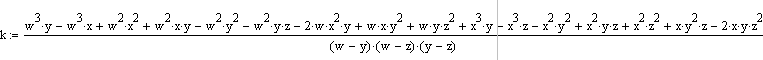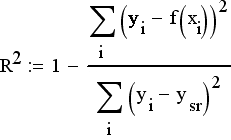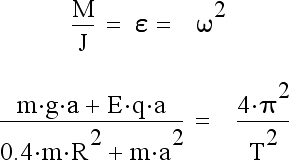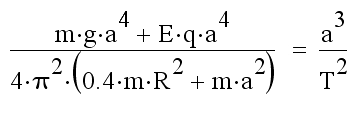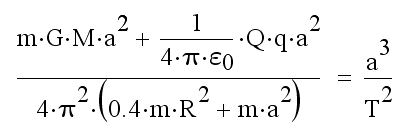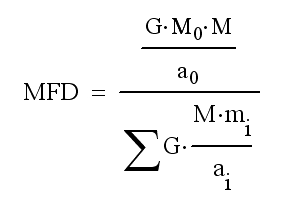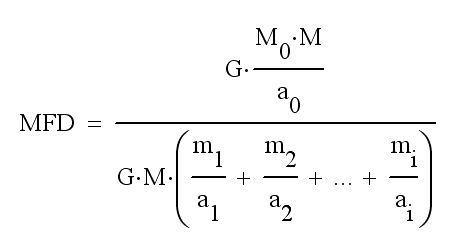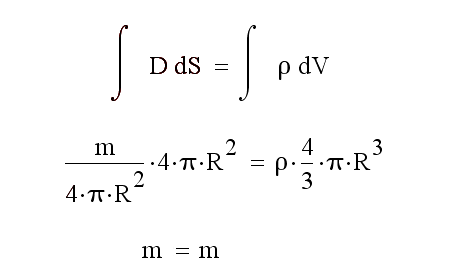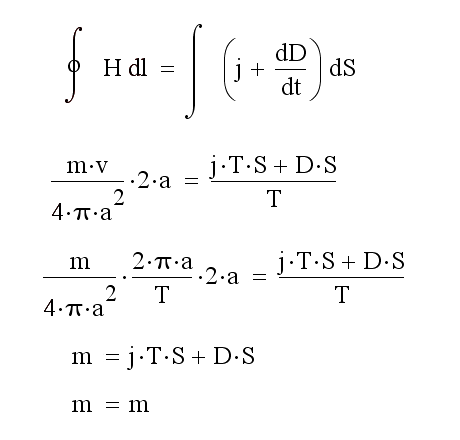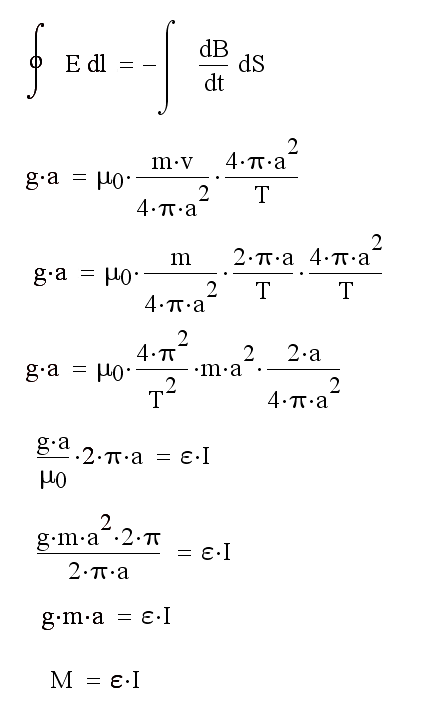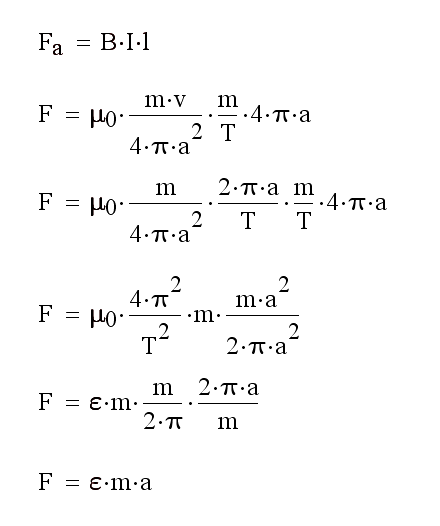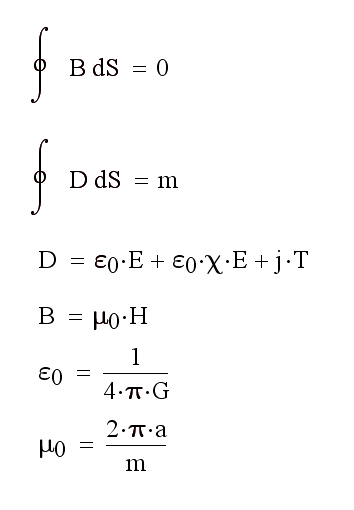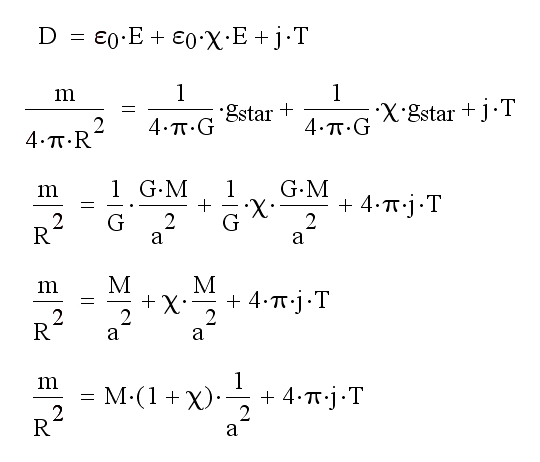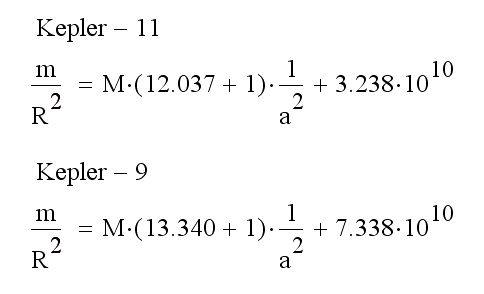Данные на 7 июня 2011
0. Общие положения.
Планета - тело без ядерных реакций с массой, позволяющей принять сферическую форму, и с гравитационным разделением вещества. Объекты спектральных классов Т и L без ядерных реакций также будут планетами. Планета может вращаться вокруг звезды или быть самостоятельным телом. Теоретически существуют кратные планетные системы. По строению планеты можно разделить на планеты земной группы и газовые гиганты с плавным переходом между ними. Разброс параметров планет на апрель 2008 года: масса примерно от 0.000173 до 13 масс Юпитера, плотность от 222 до 12500 кг/м
3, радиус от 2400 до 137270 км, радиус орбиты от 0.0177 до 30 а. е., температура верхнего слоя от 30 до 2700 К. Данные по планетам Солнечной системы и экзопланетам размещены в интернете на соответствующих сайтах и доступны всем желающим, научные работы размещены на сайте
arxiv.org/astro-ph/. Российский сайт по экзопланетам я знаю только один -
www.allplanets.ru.
Для сравнения между собой звёздных систем с разной массой звезды и планетных систем с разной массой планет мной была придумана система относительного сравнения, позволяющая в одном масштабе сравнивать планеты, спутники и все остальные тела. Первый параметр U показывает отношение массы зависимого тела (которое обращается, планета или спутник) к массе центрального тела (вокруг которого обращается, звезда или планета): U=lg(m/M), M - масса центрального тела в килограммах, m - масса планеты или спутника в килограммах, чем меньше параметр U тем больше разница в массах. Параметр U всегда меньше нуля. Классификация тел в зависимости от параметра U (рис. 1).
 Рис. 1. Классификация тел по параметру U.
Рис. 1. Классификация тел по параметру U.
В соответствии с этой классификацией Меркурий и Марс будут U7, Земля и Венера U6, Юпитер и Сатурн U4, Уран и Нептун U5, Церера U10, Плутон U9.
Второй параметр W показывает отношение радиуса орбиты зависимого тела к массе центрального тела: W=lg(M/a)/lg(M), M - масса центрального тела в килограммах, a - радиус орбиты планеты или спутника в метрах. Параметр W всегда находится в промежутке от нуля до одного.
Параметр U я откладываю по горизонтали, параметр W по вертикали, это более наглядно чем наоборот. Если в этих координатах (U - W) отобразить все планеты Солнечной системы и все спутники с известными массами, то получится планетная диаграмма Солнечной системы (рис. 2).
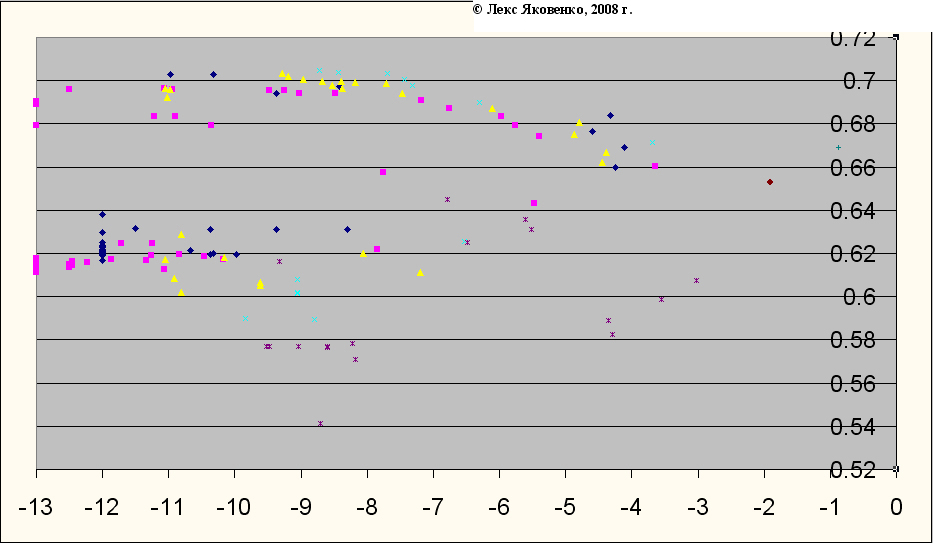 Рис. 2. Планетная диаграмма Солнечной системы. По горизонтали параметр U, по вертикали параметр W.
Рис. 2. Планетная диаграмма Солнечной системы. По горизонтали параметр U, по вертикали параметр W.
Проведём кривую через нижние граничные точки - это нижняя планетная кривая, все тела в системе находятся выше её. Ниже нижней планетной кривой тела находится не могут из-за гравитационного взаимодействия с планетами - их орбиты будут неустойчивыми и изменяться так, что будут выше нижней планетной кривой.
Через верхние граничные точки проведём кривую и назовём верхней планетной кривой, все тела в системе находятся ниже её. Выше верхней планетной кривой тела находится не могут опять же из-за приливных сил - слишком близко к планетам и звезде приближаться нельзя. Всё вместе является графическим представлением гравитационных сил в системе (в данном случае в Солнечной системе, рис. 3).
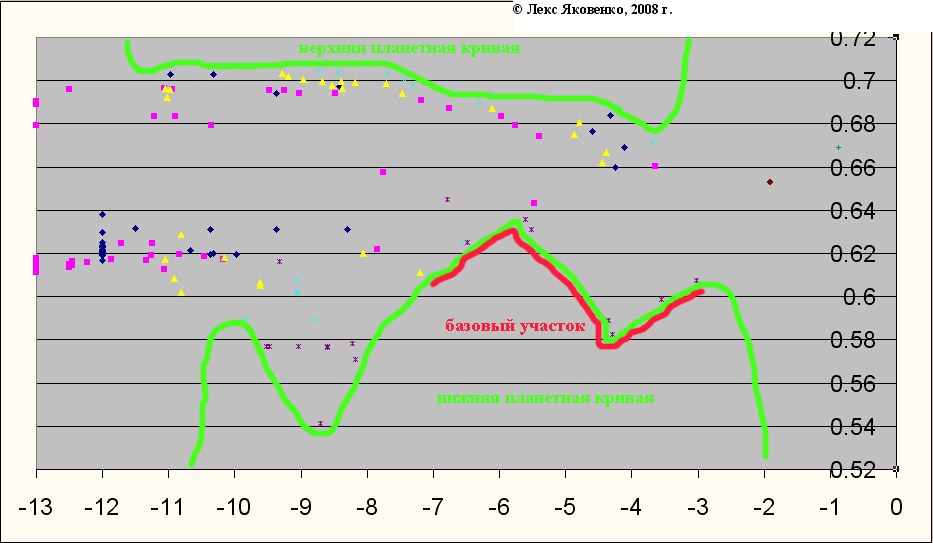 Рис. 3. Планетные кривые Солнечной системы.
Рис. 3. Планетные кривые Солнечной системы.
Планетные кривые показаны зелёным цветом. Теоретически правые части нижней и верхней планетных кривых могут соединяться, огибая спутники-супергиганты (на рис. 3 их всего два: Луна и Харон). Для мелких спутников планет Солнечной системы в левой части диаграммы, масса которых неизвестна, параметр U условно принят в -12, -12.5 и -13. Левые части нижней и верхней планетных кривых также могут соединяться, огибая все мелкие тела на всех орбитах, что в действительности вряд ли может быть точно определено. На рис. 2 показаны 8 планет, Церера, 8 плутонов, все известные спутники планет-гигантов, Луна и Харон (спутник Плутона). Спутники Марса и плутонов (кроме одного) не показаны, кольца планет-гигантов не показаны (они будут гораздо левее и немного выше), пояс астероидов не показан, астероиды пояса Койпера и облака Оорта не показаны. Как видно из диаграммы спутники не выходят за пределы нижней планетной кривой построенной по точкам планет и плутонов (нижняя граница спутников не выходит за линию планет и плутонов). Красным цветом отмечен базовый участок нижней планетной кривой, который выглядит примерно симметричным зеркальной симметрией с поворотом.
Планетную диаграмму можно построить для любой системы, в которой вокруг центрального тела что-нибудь вращается, даже если это частицы звёздного ветра. На планетной диаграмме можно показать все тела и образования в системе, какими бы они не были.
1. Способы обнаружения планет.
На апрель 2008 года мне известны следующие способы обнаружения планет:
1) Визуальный способ - планета обнаруживается визуально невооружённым или вооружённым глазом. Этим способом обнаружены все планеты Солнечной системы кроме Нептуна и все большие спутники планет. Современная техника позволяет получать фотографии звёзд, на которых видны горячие гиганты. Способ пригоден для всех планет, но с увеличением дистанции мелкие планеты становятся не видны (только для тусклых звёзд и больших планет).
1а) Визуально-программный способ - сперва делается фотография звезды или сразу группы звёзд, затем программными средствами из изображения каждой звезды вытягивается информация о всех объектах. Необходимо минимум два снимка, чтобы отличить наложившиеся объекты от связанных гравитацией.
2) Способ гравитационных возмущений - сперва обнаруживают гравитационные возмущения в движении известных тел, на основе возмущений рассчитывают параметры планеты и подтверждают её существование визуально. Этим способом был открыт Нептун. Способ пригоден для любых планет.
3) Способ тайминга звёздных пульсаций - по периодическим изменениям в излучении пульсаров. Этим способом были открыты планеты с массой 0.02 массы Земли. Способ работает только для пульсаров.
4) Спектральный способ - планеты-гиганты своей гравитацией оказывают небольшие периодические влияния на спектральные линии звезды, по этим данным рассчитывают параметры планеты. Способ пригоден только для горячих гигантов.
5) Способ колебаний звезды - звезда и планета вращаются вокруг общего центра масс, если планета большая и звезда маленькая, то звезда будет бултыхаться относительно других звёзд на небесной сфере. По данным колебания звезды рассчитывают параметры планет. Способ пригоден только для маленьких звёзд и больших планет.
6) Транзитный способ - при проходе планеты по диску родной звезды, блеск звезды снижается. По данным изменения блеска звезды рассчитывают параметры планеты, для близких звёзд и планет-гигантов получены фотографии транзитов. Метод пригоден для тусклых звёзд и больших планет, плоскость вращения которых ориентирована боком к наблюдателю на Земле.
7) Способ измерения звёздной активности - движение планет вокруг звезды оказывают влияние через гравитационное и электромагнитное поля на звезду, изменяются светимость звезды, уровень излучения, осесимметричное крупномасштабное магнитное поле, появляются и исчезают корональные дыры. Анализируя весь массив данных можно определить сколько планет вращается вокруг звезды и их параметры. Метод пригоден для любых звёзд, у которых регистрируется активность, и любых планет вне зависимости от периода обращения, единственное ограничение - долгий срок наблюдения. Чем больше короткопериодичных планет в системе тем быстрее и точнее метод.
2. Метод расчёта радиусов планет.
Сразу же нужно упомянуть правило Тициуса-Боде, описывающее радиус орбиты планет Солнечной системы как зависимость от порядкового номера, считая от Солнца к поясу Койпера. Радиус орбиты планеты a=0.4+0.3*2
n, в астрономических единицах, для Меркурия n=-∞, для Венеры n=0 и т. д., но уже для Нептуна правило не работает. Эту закономерность астрономы Тициус и Боде нашли эмпирически, физико-математического объяснения этой закономерности пока нет. Аналоги правила Тициуса-Боде можно подобрать для сферических спутников планет-гигантов в Солнечной системе.
В мае-июне 2008 г. мной была найдена закономерность между радиусами орбиты планет, межпланетными расстояниями и внутренним радиусом пояса Койпера.
На графике по горизонтали отложим радиусы планет (большой разницы какой радиус брать - в афелии, перигелии или средний, нет, т. к. планеты обмениваются эксцентриситетами и в многотысячелетнем временном обзоре видны колебания планет около определённого радиуса),
а по вертикали отложим расстояние между двумя ближайшими планетами. Все расстояния в астрономических единицах. Данные Меркурия не используем -
об этой планете разговор отдельный.
| планета |
радиус орбиты, а.е. |
расстояние до следующей планеты, а.е. |
| Венера |
0.723 |
0.277 |
| Земля |
1.000 |
0.524 |
| Марс |
1.524 |
1.241 |
| пояс астероидов - Церера |
2.765 |
2.438 |
| Юпитер |
5.203 |
4.336 |
| Сатурн |
9.539 |
9.644 |
| Уран |
19.183 |
10.875 |
Аппроксимацией этих точек является парабола, пересекающая ось ОХ в двух точках, дальняя точка от начала координат предположительно является предельным радиусом формирования планет и примерно совпадает с началом пояса Койпера.
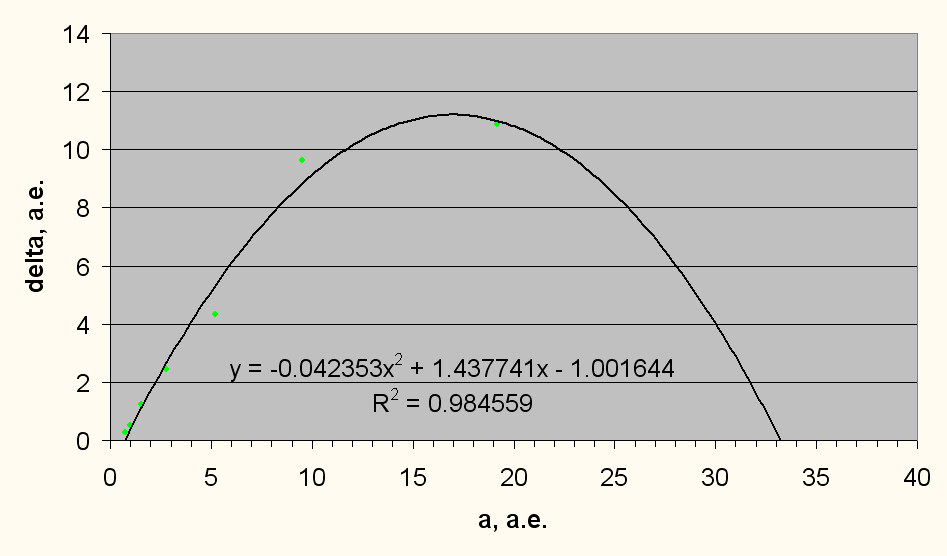 Рис. 4. Зависимость расстояния между планетами от радиуса орбиты планет.
Рис. 4. Зависимость расстояния между планетами от радиуса орбиты планет.
Радиус начала пояса Койпера в астрономии принят равным орбите Нептуна - 30 а.е., это значение сильно отличается от предельного радиуса формирования планет. По радиусам орбит объектов пояса Койпера можно предположить, что предельный радиус формирования планет для Солнечной системы будет примерно 38 а.е.
Сравним внутренний радиус поясов Койпера некоторых звёзд с их массой:
| звезда |
радиус, а.е. |
масса звезды |
| Вега, HD 172167 |
58.2a |
2.11a |
| Фомальгаут, HD 216956 |
57.5b |
2b |
| Солнце |
38 |
1 |
| 55 Cancri, HD 75732 A |
38c |
0.95c |
| eps Eridani, HD 22049 |
35d |
0.85d |
a - K. Y. L. Su et al., astro-ph/0504086; b - P. Kalas et al., astro-ph/0506574; c -
страница 55 Cnc на сайте wikipedia.org, радиус условно равен солнечному; d -
страница eps Eridani на сайте wikipedia.org, также смотрите страницу
Debris disc и ссылки внизу на сайте wikipedia.org
Разумеется, это весьма приблизительные значения предельных радиусов, т.к. наблюдения пылевых дисков звёзд проводились на разных длинах волн, плюс изменение внутреннего радиуса пылевого диска при эволюции звезды.
Зависимость предельного радиуса формирования планет от массы звезды можно апроксимировать прямой a=18.562Ms+19.688, для всех масс звёзд от 0.012 до 100 масс Солнца этот график, скорее всего, будет параболой, который в диапазоне 0.85 - 2.11 масс Солнца может быть заменён прямой.
По этой формуле для Солнца предельный радиус формирования планет будет 38.3 а.е. Также можно предположить что все звёзды имеют одинаковое ускорение свободного падения в точке предельного радиуса формирования планет, и тогда R=(GM/g)
0.5, за эталон можно принять g Солнца при радиусе 38.0-38.4 а.е. С учётом этого таблица зависимости межпланетного расстояния от радиусов планет примет вид:
| планета |
радиус орбиты, а.е. |
расстояние до следующей планеты, а.е. |
| Венера |
0.723 |
0.277 |
| Земля |
1.000 |
0.524 |
| Марс |
1.524 |
1.241 |
| пояс астероидов - Церера |
2.765 |
2.438 |
| Юпитер |
5.203 |
4.336 |
| Сатурн |
9.539 |
9.644 |
| Уран |
19.183 |
10.875 |
| Нептун |
30.058 |
8.242 |
| пояс Койпера |
38.3 |
0 |
График будет выглядеть как:
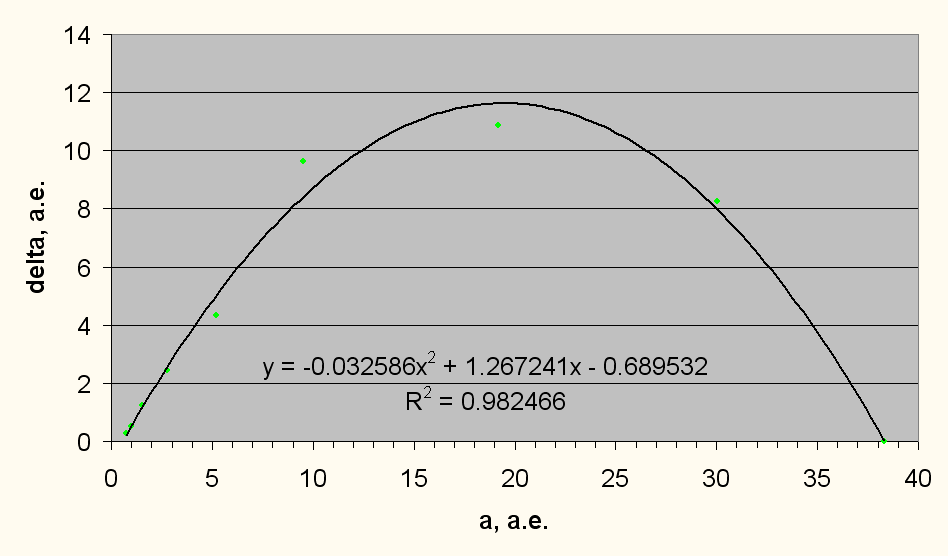 Рис. 5. Зависимость расстояния между планетами от радиуса орбиты планет и предельного радиуса формирования планет, примерно совпадающего с внутренним радиусом пояса Койпера.
Рис. 5. Зависимость расстояния между планетами от радиуса орбиты планет и предельного радиуса формирования планет, примерно совпадающего с внутренним радиусом пояса Койпера.
Теперь рассмотрим возможность построения параболы по нескольким точкам и нахождения параметров орбиты остальных планет из параболы.
Если строить параболу Солнечной системы по данным первых трёх планет (два межпланетных интервала) и предельному радиусу формирования планет - всего три точки, то по полученной параболе получается 11 планет в системе - явная ошибочность параболы.
Если строить параболу по первым четырём планетам и предельному радиусу формирования планет - всего четыре точки, то в системе получается 8 планет, что является верным результатом.
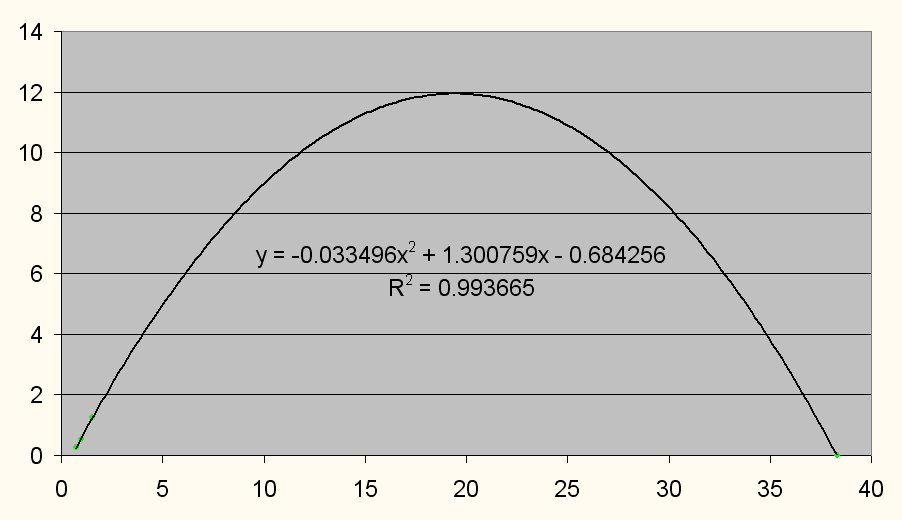 Рис. 6. Парабола Солнечной системы по первым четырём планетам и предельному радиусу формирования планет - 4 точки.
Рис. 6. Парабола Солнечной системы по первым четырём планетам и предельному радиусу формирования планет - 4 точки.
| известные радиусы орбиты планеты, а.е. |
рассчитанные расстояния между планетами, а.е. |
рассчитанные радиусы орбиты планеты, а.е. |
реальные радиусы орбиты планеты, а.е. |
| 0.723 |
0.277 |
|
|
| 1.000 |
0.524 |
|
|
| 1.524 |
1.241 |
|
|
| 2.765 |
2.656 |
|
|
| |
5.383 |
5.421 |
5.203 |
| |
9.459 |
10.804 |
9.539 |
| |
11.957 |
20.263 |
19.183 |
| |
6.551 |
32.220 |
30.058 |
| 38.3 |
|
38.771 |
|
Парабола пересекает ось ОХ в двух точках, дальняя точка является предельным радиусом формирования планет, за этим радиусом планеты не формируются. Ближняя точка также имеет физический смысл, Меркурий находится за пределами интервала параболы (0.552 а.е - 38.337 а.е.).
Эта методика позволяет рассчитать параметры орбиты ещё не открытых планет для звёзд у которых определена масса и открыты четыре планеты, лежащие внутри диапазона параболы (между точками пересечения параболы с осью ОХ). Планеты должны располагаться подряд, одна за другой без промежутков. Также мной разработана эмпирическая методика подбора наиболее вероятных орбит неоткрытых планет в промежутках между открытыми планетами. Поэтому комбинированная методика применима для звёзд с открытыми двумя планетами (пояса астероидов тоже учитываются), расположенными внутри интервала параболы (грубо от 0.6 до 10 а.е.), которых на сегодняшний день 03.07.2008 уже больше десятка. Подробные рассчёты каждой системы смотрите на этом сайте на соответствующих страничках, доступных через
список звёздных систем.
3. Алгоритм оптимизации построения параболы для системы с двумя известными планетами на примере Солнечной системы.
Для четырёх планет всё предельно понятно, об этом написано выше. Известны две планеты, а нужно минимум четыре, две планеты придётся задавать эмпирически. Возможны три случая:
1. две неизвестные планеты располагаются между известными планетами,
2. одна неизвестная планета располагается между известными планетами, а вторая неизвестная планета находится справа или слева (на графике радиусов орбит) от известных планет,
3. две известные планеты расположены подряд и между ними запихать планеты не получается, две неизвестные планеты располагаются справа или слева (на графике радиусов орбит) от известных планет, в этом случае выбираем сами, как расположить неизвестные планеты, можно даже одну сделать слева, а вторую справа от известных.
Всего возможно 6 вариантов расположения 2 неизвестных планет относительно 2 известных:
| n/n |
вариант 1 |
вариант 2 |
вариант 3 |
вариант 4 |
вариант 5 |
вариант 6 |
| 1 |
рп 1 |
нп 1 |
нп 1 |
рп 1 |
нп 1 |
рп 1 |
| 2 |
рп 2 |
рп 1 |
нп 2 |
нп 1 |
рп 1 |
нп 1 |
| 3 |
нп 1 |
рп 2 |
рп 1 |
рп 2 |
нп 2 |
нп 2 |
| 4 |
нп 2 |
нп 2 |
рп 2 |
нп 2 |
рп 2 |
рп 2 |
рп - реальная планета, нп - неизвестная планета, нумерация планет от звезды.
Важно, что вместо реальной планеты можно использовать реальный пояс астероидов, который легче обнаружить чем планету.
По условиям нам известны два объекта в системе: планета с орбитальным радиусом 0.723 а.е. и пояс астероидов с орбитальным радиусом 2.765 а.е., реально конечно же будет проблематично так точно установить правильный орбитальный радиус для пояса астероидов. Для пояса астероидов Солнечной системы обзор даст интервал орбитальных радиусов 2-4 а.е., средний орбитальный радиус будет 3 а.е., предположим, что происходит смещение к звезде истинного орбитального радиуса. Естественно, это условность и как она сработает для поясов астероидов в других системах - неизвестно, надо разбираться с каждым случаем индивидуально.
Предположим, реальный орбитальный радиус для пояса астероидов выяснили. Если это планета то тем лучше. Итого у нас есть:
| планета |
радиус орбиты, а.е. |
масса звезды |
| планета 1 |
0.723 |
1 |
| планета 2 |
2.765 |
1 |
Масса звезды нам известна и равна 1 солнечной, по уравнению a=18.562*Ms+19.688 считаем предельный радиус формирования планет для этой звезды (масса звезды должна быть в интервале 0.85-2 массы Солнца, а то придётся вводить поправки - для всех масс звёзд график парабола). Для нашей звезды радиус равен 38.25 а.е.
Теперь считаем параметр W для известных планет, W=log(M/a)/logM, где М - масса звезды в килограммах, а - радиус орбиты в метрах. Получается:
| планета |
радиус орбиты, а.е. |
масса звезды |
параметр W |
| планета 1 |
0.723 |
1 |
0.635823 |
| планета 2 |
2.765 |
1 |
0.616596 |
Округляем W до тысячных, получается 0.636 для первой планеты и 0.617 для второй планеты, от первого W отнимаем второе W: 0.636-0.617=0.019 - это разность между планетами. Среднее значение разности примерно 0.008 и в нашем примере не подходит - значит между планетами должна быть ещё планета или две. Смотрим на массы планет, если они определены и находим по рисунку 1 U-класс планет и соответствующий подкласс. Теперь смотрим таблицу расстояний в разности параметра W:
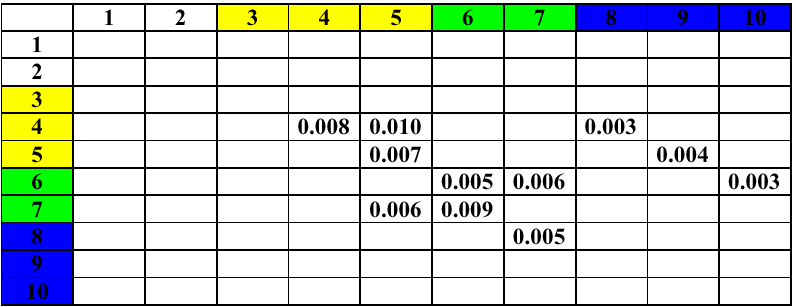 Рис. 7. Зависимость расстояния между планетами от разности параметра W для Солнечной ситемы.
Рис. 7. Зависимость расстояния между планетами от разности параметра W для Солнечной ситемы.
Найденное значение переводим в астрономические единицы. Таблица составлялась по телам Солнечной системы, и, скорее всего, если массы планет не определены, окажется бесполезной. В дальнейшем эти значения скорректируются.
Предположим, что между нашими 2 известными планетами находится одна неизвестная. Разность 0.019 нужно поделить на две части, например на 0.010 и 0.009, большой разницы как поделить нет - главное примерно поровну, можно и 0.009 и 0.010, можно и 0.0095 и 0.0095. Я выбрал первый вариант, получается 0.636, 0.626 и 0.617. Нужна четвёртая планета, пусть она будет справа (на графике), используем стандарную разность 0.008, получается 0.609 у второй неизвестной планеты. Переводим параметр W в астрономические единицы, считаем разность в астрономических единицах (радиус орбиты планеты n+1 минус радиус орбиты планеты n), строим параболу по точкам, получается:
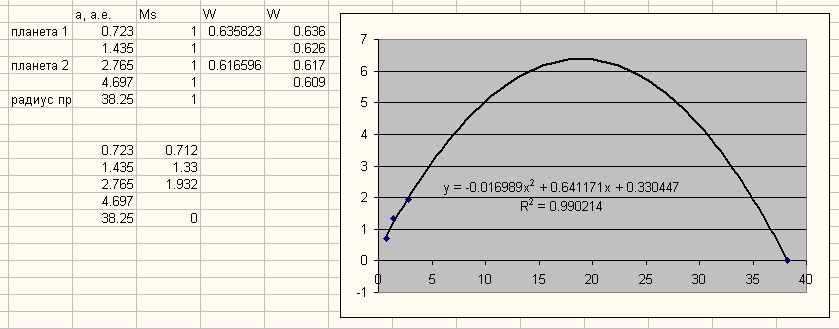 Рис. 8. Первый шаг алгоритма оптимизации.
Рис. 8. Первый шаг алгоритма оптимизации.
Высота параболы на рисунке 8 примерно 6.4, а надо только примерно 12 - при меньшей высоте точки на параболе будут расположены неправильно - в конце параболы будет много планет на очень близких орбитах, как в начале. А такого физически быть не может - пока примеров нет. Точки должны лежать классически - в конце параболы только нулевая точка, смотрите рисунок 5. Теперь подставляем вместо значения 1.435 другое значение, больше или меньше, чтобы высота параболы равнялась 12. Максимальная высота параболы в нашем случае будет примерно 6.8 при значении 1.25, больше высота не будет при любом значении радиуса первой неизвестной планеты. Радиусы орбит известных планет менять нельзя. Максимальная разность не должна превышать 0.010 W, это условный предел. Можно поробовать сдвигать радиус орбиты второй неизвестной планеты 4.697 а.е., высота параболы будет 12 при значении 5.75, но разность W превысит предел. Если при этих параметрах рассчитать остальные планеты в системе то будет ошибка.
Делаем предположение что между двумя известными планетами находятся две неизвестные планеты. Разность 0.019 делим на три примерно равные части - 0.006, 0.007 и 0.006. Параметр W у неизвестных планет будет соотвественно 0.630 и 0.623, вычисляем точки и строим параболу:
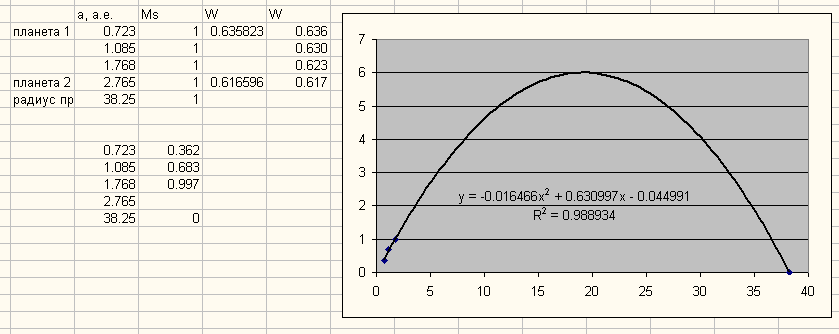 Рис. 9. Второй шаг алгоритма оптимизации.
Рис. 9. Второй шаг алгоритма оптимизации.
Теперь изменяем радиус орбиты первой неизвестной орбиты, чтобы высота параболы была максимальной, получается максимум 6.3 при радиусе 1.00 а.е., изменяем радиус орбиты второй неизвестной планеты, максимум 12 получается при радиусе 1.52 а.е., при меньшем радиусе максимум параболы превышает 12, что также ведёт к ошибке. Получается:
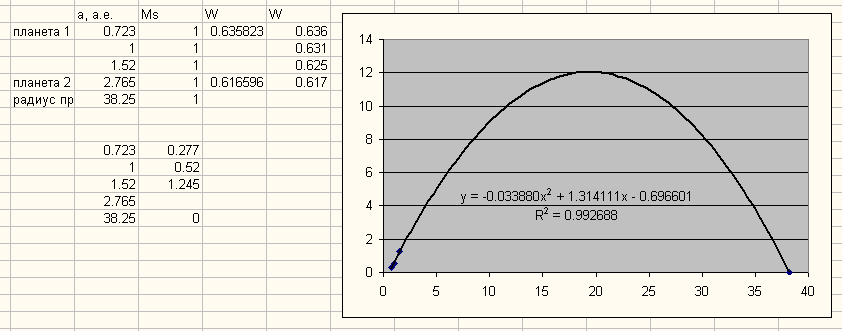 Рис. 10. Третий шаг алгоритма оптимизации.
Рис. 10. Третий шаг алгоритма оптимизации.
Переходим к расчётам орбит остальных планет в системе и одновременной проверке правильности найденной параболы. По радиусу орбиты первой планеты 0.723 и уравнению параболы рассчитываем радиусы остальных планет:
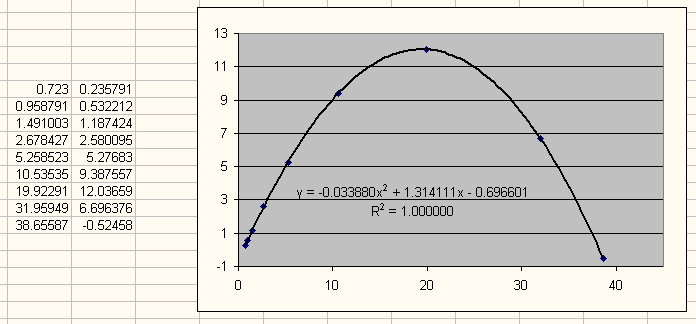 Рис. 11. Четвёртый шаг алгоритма оптимизации.
Рис. 11. Четвёртый шаг алгоритма оптимизации.
Получившиеся радиусы орбит планет и их количество соотвествуют реальным, что подтверждает правильность алгоритма оптимизации. Можно написать программу, выполняющую все расчёты и графики самостоятельно.
Теперь рассмотрим другой случай, более вероятный. Изучая нашу систему астрономы заметили планету с радиусом орбиты 5.203 а.е. и пояс астероидов с радиусом орбиты 2.76 а.е. - именно Юпитер и пояс астероидов заметить легче всего. Разность между планетами 0.009 W - между ними планету не вставить, следовательно неизвестные планеты располагаются справа или слева. Я расположил слева - ближе к звезде. Используем стандартную разность 0.008, получается известные планеты 0.617 и 0.608, и неизвестные планеты 0.625 и 0.633. Строим график:
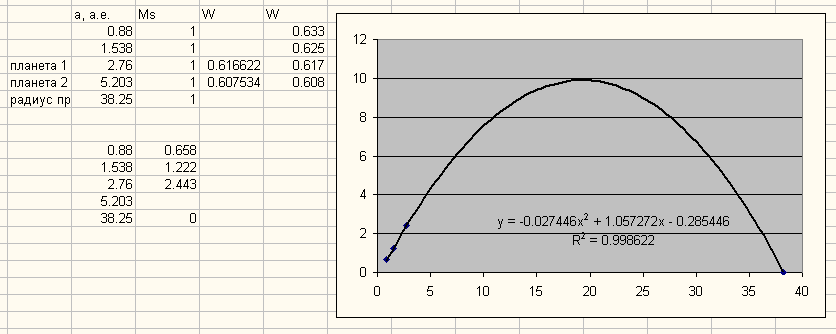 Рис. 12. Первый шаг алгоритма оптимизации.
Рис. 12. Первый шаг алгоритма оптимизации.
Изменяем радиус орбиты первой неизвестной планеты, чтобы высота параболы была 12, максимум получается при радиусе орбиты 1.12 а.е.:
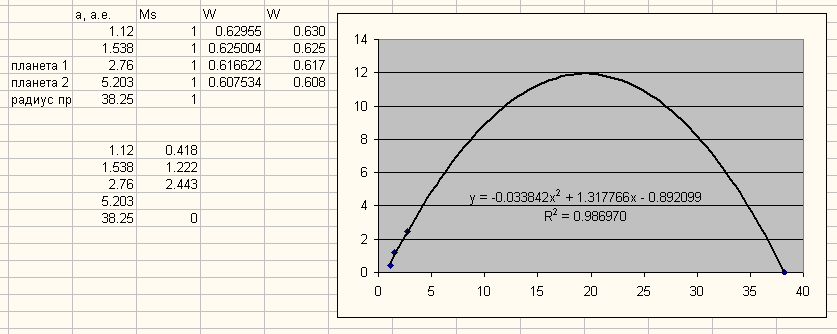 Рис. 13. Первый шаг алгоритма оптимизации.
Рис. 13. Первый шаг алгоритма оптимизации.
По найденной параболе считаем все орбиты планет в системе, получается:
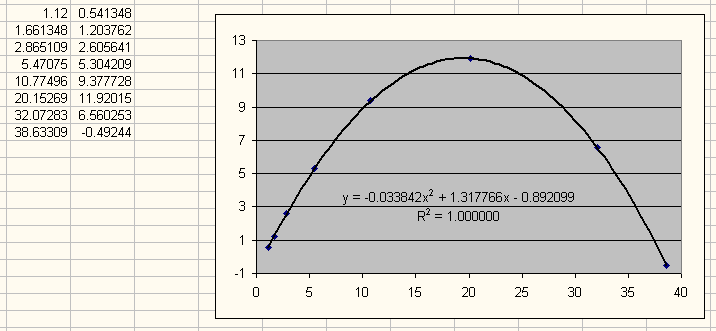 Рис. 14. Итоговый результат.
Рис. 14. Итоговый результат.
Как видно на рисунке 14 радиусы орбит планет получились с большей погрешностью чем в предыдущем случае, но всё же достаточно верно. Радиусы орбит известных планет не совпали с рассчитанными значениями, поэтому полученную параболу можно дополнительно оптимизировать, добиваясь совпадения известных радиусов орбит с рассчётами, но высота параболы не должна отклоняться от 12. Расчёты показывают, что в данном случае погрешность в расчётах радиусов орбит всех планет возникает именно из-за использования орбитального радиуса Юпитера, который расположен далеко от левого края параболы - предпочтительнее использовать орбитальные радиусы планет в диапазоне 0.6-3 а.е.
Если подходят несколько вариантов, то проверяют по орбитальному радиусу предыдущей планеты (ближе к звезде, чем первая использованная в расчётах). Для рисунка 14 это будет планета перед планетой с орбитальным радиусом 1.12 а.е. Решаем систему уравнений:
x+y=1.12
y=1.12-x
1.12-x=-0.033842x
2+1.317766x-0.892099
-0.033842x
2+2.317766x-2.012099=0
корнями этого уравнения являются x
1=67.608 а.е. и x
2=0.879 а.е.,
второй корень является верным.
Лучше будет вариант, в котором планета будет более правдоподобной.
4. Метод расчёта радиусов для горячих гигантов.
Парабола для обычных планет в Солнечной системе находится на отрезке 0.552 - 38.25 а.е., ближе к звезде на отрезке 0 - 0.552 а.е. находится парабола для горячих гигантов. Далее 38.25 а.е. может находится ещё одна парабола, пока это не проверял.
Я 20 июля 2008 г. исследуя системы с несколькими планетами на параболе для горячих гигантов подтвердил данными правильность моего предположения. Действительно радиусы орбит планет и расстояния между ними образуют две параболы - малую и большую. Для Солнечной системы малая парабола (для горячих гигантов) будет выглядеть как:
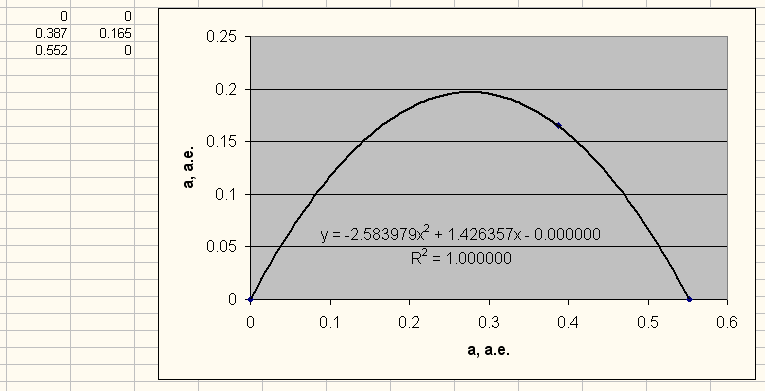 Рис. 15. Малая парабола (для горячих гигантов) Солнечной системы. Точкой отмечен Меркурий и пересечения с осью ОХ.
Рис. 15. Малая парабола (для горячих гигантов) Солнечной системы. Точкой отмечен Меркурий и пересечения с осью ОХ.
В Солнечной системе на малой параболе находится только Меркурий, остальные планеты находятся на большой параболе. Обе параболы для Солнечной системы будут выглядеть как:
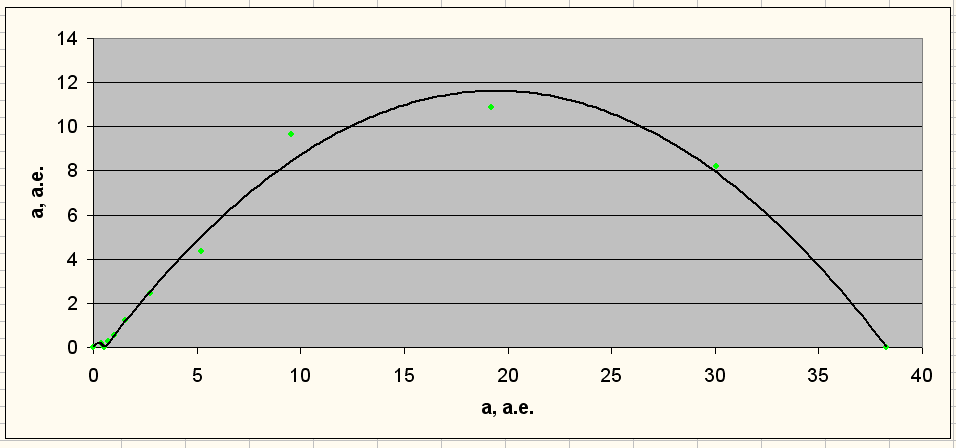 Рис. 16. Две параболы Солнечной системы. Точками отмечены планеты и пересечения с осью ОХ.
Рис. 16. Две параболы Солнечной системы. Точками отмечены планеты и пересечения с осью ОХ.
Расчёт орбитальных радиусов планет на малой параболе (для горячих гигантов) присходит по оптимизированному алгоритму, описанному выше. Также расстояние между планетами в среднем 0.008 W. Для примера приведу малую параболу для системы HD 40307:
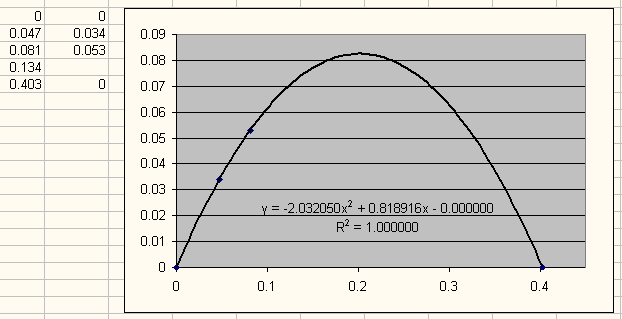 Рис. 17. Малая парабола системы HD 40307. Точками отмечены планеты и пересечения с осью ОХ.
Рис. 17. Малая парабола системы HD 40307. Точками отмечены планеты и пересечения с осью ОХ.
В системе HD 40307 на малой параболе находятся три планеты с радиусами орбит 0.047, 0.081 и 0.134 а.е., и существуют ещё не открытые планеты.
Для системы 55 Cnc малая парабола будет:
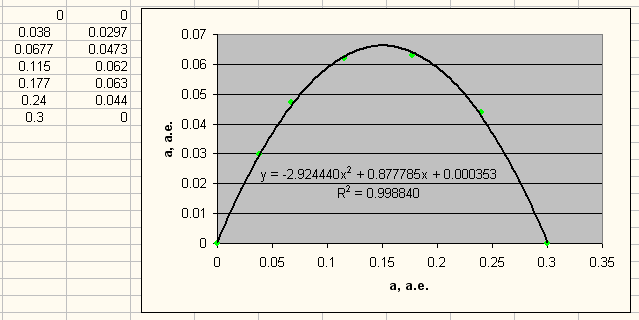 Рис. 18. Малая парабола системы 55 Cnc. Точками отмечены планеты и пересечения с осью ОХ.
Рис. 18. Малая парабола системы 55 Cnc. Точками отмечены планеты и пересечения с осью ОХ.
В этой системе добавлены две неизвестные планеты с радиусами орбит 0.0677 и 0.177 а.е.
Используя две параболы и оптимизированный алгоритм расчёта радиусов планетных орбит теперь возможно точно рассчитать любую систему с двумя планетами на второй параболе и с двумя или тремя планетами на первой параболе.
Для построения каждой параболы в методе используются пять точек: радиусы орбит двух реальных планет А и B, радиусы орбит двух предполагаемых планет C и D, и предельный радиус формирования планет E. Две предполагаемые планеты расположены после второй реальной планеты. Вторая координата рассчитывается как радиус последующей минус радиус предыдущей орбиты. Запишем эти точки:
A (z;w-z)
B (w;x-w)
C (x;k-x)
D (k;...)
E (y;0)
Из пяти радиусов орбит получаются четыре точки, точка D без второй координаты. Эти точки лежат на параболе, уравнение параболы f=-ax
2+bx-c. Парабола находится в первой четверти координат, ветви направлены вниз, вершина параболы находится в точке М (х
0;12) - высота параболы всегда 12 (найдено эмпирически). Точка М это экстремум функции и максимум. В точке экстремума первая производная равна нулю: -2ax
0+b=0, выразим икс нулевое x
0=b/2a. Подставляем координаты точки М в уравнение параболы, получается: 12=-a*b
2/4a
2+b*b/2a-c. Упрощаем выражение, получается: b
2-4ac-48a=0. Это условие при котором высота параболы будет 12. Теперь подставляем координаты точек A, B, C, E в уравнение параболы. С учётом условия на высоту получается система из пяти уравнений:
w-z=-az2+bz-c (1)
x-w=-aw2+bw-c (2)
k-x=-ax2+bx-c (3)
-ay2+by-c=0 (4)
b2-4ac-48a=0 (5)
Из этой системы уравнений выражаем переменные a, b, c, x, k через числа z, w, y. Выражения для a, b, c нам пока не важны (график строится по точкам на компьютере), а вот выражения для x и k пригодятся. Выражение для x:
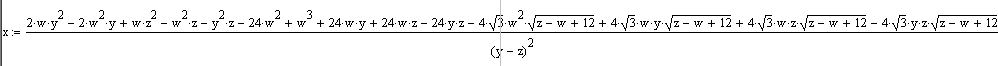 Рис. 19. Математическое выражение радиуса орбиты (x) первой предполагаемой планеты через радиусы орбит (z, w) двух известных планет и предельного радиуса (y) формирования планет.
Рис. 19. Математическое выражение радиуса орбиты (x) первой предполагаемой планеты через радиусы орбит (z, w) двух известных планет и предельного радиуса (y) формирования планет.
При решении системы уравнений получаются два выражения для х (вторая степень у х, два корня при решении), но во втором выражении значения х не подходят - радиус орбиты получается слишком близким к радиусу орбиты предыдущей планеты. Выражение для k одно:
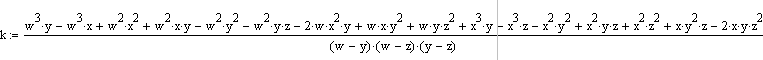 Рис. 20. Математическое выражение радиуса орбиты (k) второй предполагаемой планеты через радиусы орбит (z, w) двух известных планет и предельного радиуса (y) формирования планет.
Рис. 20. Математическое выражение радиуса орбиты (k) второй предполагаемой планеты через радиусы орбит (z, w) двух известных планет и предельного радиуса (y) формирования планет.
Сделаем проверку для радиусов орбит Венеры, Земли и предельного радиуса формирования планет в Солнечной системе: z=0.723, w=1.000, y=38.3. Получается x=1.622, k=3.000. По рассчитанным точкам строим большую параболу:
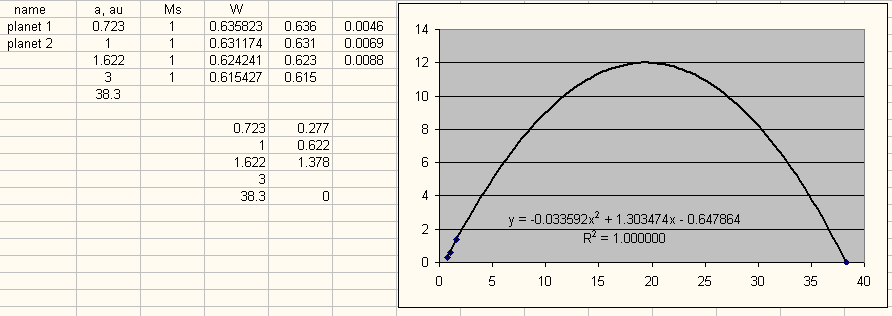 Рис. 21. Большая парабола по рассчитанным точкам.
Рис. 21. Большая парабола по рассчитанным точкам.
Как видно на рисунке 21, рассчитанные значения x и k соответствуют равновесной точке, при которой коэффициент детерминации R
2 равен единице. Существуют другие пары значений x и k, для которых высота параболы также 12, но коэффициент детерминации R
2 отклоняется от единицы. При этом пара значений x и k должны находится в диапазоне разности W двух ближайщих планет, 0.0047<=W
n+1-W
n<=0.011. Значение 0.0047 это разность W между Землёй и Венерой (планеты земного типа могут быть расположены очень близко друг к другу), значение 0.011 это разность W между массивными планетами. Для рассматриваемого случая диапазон пар значений x и k и их коэффициенты детерминации будут следующими:
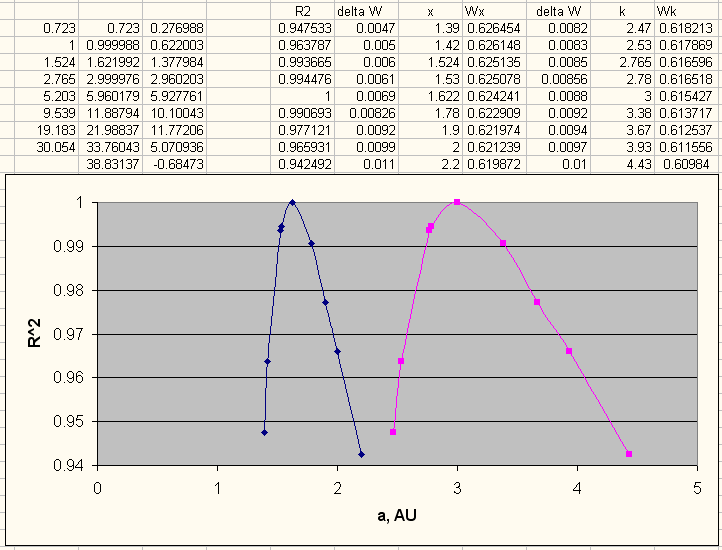 Рис. 22. Диапазон пар значений x и k и их коэффициент детерминации R2.
Рис. 22. Диапазон пар значений x и k и их коэффициент детерминации R2.
Также на рисунке 22 показаны рассчитанные радиусы орбит всех планет на большой параболе Солнечной системы для равновесной точки. Реальные радиусы орбит Марса и Цереры находятся в 0.99- интервале R
2. Для анализа расположения возможных планетных орбит Я буду указывать пять вариантов с R
2 0.98-,0.99-,1.00,0.99+,0.98+. Радиусы орбит планет на указанном промежутке значений R
2 смещаются по параболе от начала к предельному радиусу формирования планет.
Коэффициент детерминации считается по формуле:
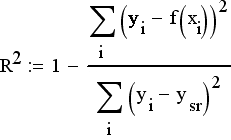 Рис. 23. Формула рассчёта коэффициента детерминации R2.
Рис. 23. Формула рассчёта коэффициента детерминации R2.
По условию R
2 равно 0.98, 0.99 (1.00 уже нашли), плюс условие 0.0047<=W
n+1-W
n<=0.011, эти два условия добавляем в систему уравнений, получается:
w-z=-az2+bz-c (1)
x-w=-aw2+bw-c (2)
k-x=-ax2+bx-c (3)
-ay2+by-c=0 (4)
b2-4ac-48a=0 (5)
1-((w-z-(-az2+bz-c))2+(x-w-(-aw2+bw-c))2+(k-x-(-ax2+bx-c))2+(-ay2+by-c)2)/((w-z-(1/4)(k+y-z))2+(x-w-(1/4)(k+y+z))2+(k-x-(1/4)(k+y-z))2+((1/4)(k+y-z))2)=0.99 (6)
0.047<=ln(M/w)/lnM-ln(M/x)/lnM<=0.011 (7)
Из этой системы уравнений и неравенств выражаем a, b, c, x, k через w,y,z. В (7) надо M перевести в килограммы, а w и x в метры. Потом в (6) меняем равенство на 0.98 и заново выражаем a, b, c, x, k через w,y,z. В итоге получится пять парабол и координат для всех выше обозначенных вариантов R
2.
Эмпирически нашли влияние высоты параболы на результат: при высоте параболы меньше 12 увеличивается количество планет и они в конце располагаются как в начале (всё ближе друг к другу), при высоте параболы больше 12 количество планет сокращается, они расположены всё дальше друг от друга:
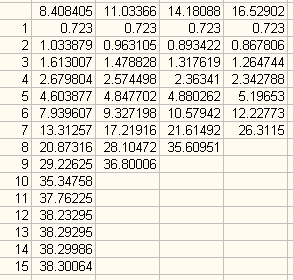 Рис. 24. Влияние высоты параболы на результат.
Рис. 24. Влияние высоты параболы на результат.
Оптимальной является высота параболы 12, отклонения в пределах +/-0.5 сильно на результат и количество планет не влияют.
6. Физические формулы.
Формула Кеплера: a
3/T
2=G(M+m)/4pi
2
Для тел, вращающихся по орбитам вокруг одного и тогоже центрального тела работает равенство a
3/T
2=константа.
Основное уравнение вращающегося тела: M/J=epsilon, где M-момент силы, J-момент инерции, epsilon-угловое ускорение. Для вращающихся тел угловое ускорение равно квадрату угловой скорости. Момент силы, действующий на планету состоит из моментов сил тяжести со свездой и всеми планетами в системе и из моментов кулоновской силы со звездой и всеми планетами в системе (у звезды и планет есть свои собственные электрические заряды). Распишем момент сил и момент инерции для планеты при взаимодействии со звездой. M=mga+Eqa. J=0.4mR
2+ma
2. Угловая скорость равна 2pi/T. В общем это выглядит как:
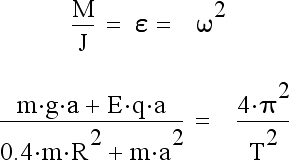 Рис. 25. Основная формула вращающегося по орбите тела.
Рис. 25. Основная формула вращающегося по орбите тела.
m-масса планеты, кг, g-ускорение свободного падения звезды на удалении орбитального радиуса планеты, м/с
2, a-орбитальный радиус планеты, м, E-напряжённость электрического поля, В/м, q-заряд планеты, Кл, R-радиус планеты, м, pi=3.1415, T-период обращения планеты по орбите вокруг звезды, с.
Для Земли формула работает. Теперь домножим обе части формулы на a
3 и разделим на 4pi
2. Справа получим выражение a
3/T
2, а это константа. Значит левая часть тоже будет константой для всех тел, вражающихся вокруг одного и тогоже центрального тела:
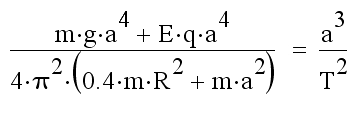 Рис. 26. Вторая формула вращающегося по орбите тела.
Рис. 26. Вторая формула вращающегося по орбите тела.
Если расписать g=GM/a
2 и E=1/4pi*eps
0*Q/a
2, то получится:
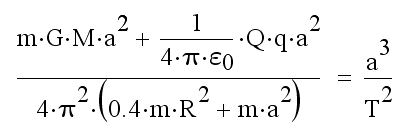 Рис. 27. Третья формула вращающегося по орбите тела.
Рис. 27. Третья формула вращающегося по орбите тела.
Теперь если известна масса планеты и её радиус, то можно вычислить произведение заряда планеты на заряд звезды Q*q. Если откинуть слагаемые с меньшими степенями и сократить подобные, то получится формула Кеплера.
Момент силы - произведение силы на плечо, момент силы притяжения - произведение силы притяжения на расстояние между телами. GMm/a
2 *a, будет GMm/a.:
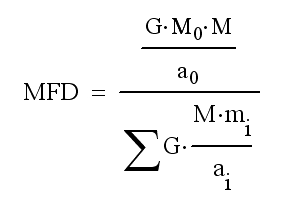 Рис. 28. Формула для расчёта отношения моментов сил притяжения.
Рис. 28. Формула для расчёта отношения моментов сил притяжения.
Где G - гравитационная постоянная, M
0 - масса звезды, M - масса планеты, a
0 - расстояние от звезды до планеты, m
i - масса i-того спутника планеты, a
i - расстояние от планеты до i-того спутника. Распишем сумму:
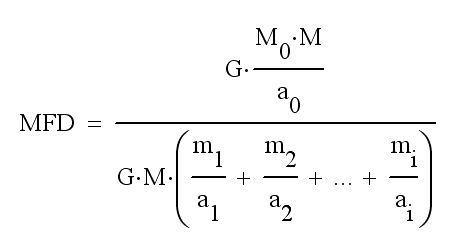 Рис. 29. Формула для расчёта отношения моментов сил притяжения с расписанной суммой.
Рис. 29. Формула для расчёта отношения моментов сил притяжения с расписанной суммой.
Сократим подобные:
 Рис. 30. Формула для расчёта отношения моментов сил притяжения после сокращения подобных.
Рис. 30. Формула для расчёта отношения моментов сил притяжения после сокращения подобных.
Из формулы следует, что отношение моментов сил притяжения не зависит от массы планеты. В Солнечной системе родные (смотрите толковник) спутники есть только у 3 планет: Юпитера, Сатурна и Урана, у Земли и Нептуна спутники не родные. Три планеты дают три точки на графике зависимости отношения моментов сил притяжения от радиуса орбиты планеты, но трёх точек мало для точности.
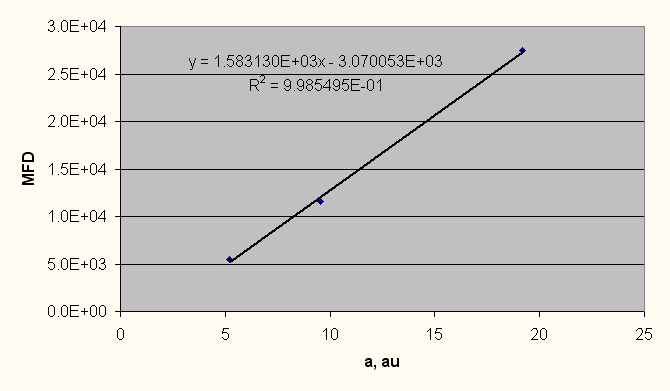 Рис. 31. График зависимости отношения моментов сил притяжения от радиуса орбиты планеты в а.е.
Рис. 31. График зависимости отношения моментов сил притяжения от радиуса орбиты планеты в а.е.
Эти точки находятся на одной прямой, по уравнению прямой рассчитаем теоретические значения отношения моментов сил притяжения для планет Солнечной системы и сравним с реальными значениями.
 Рис. 32. График зависимости отношения моментов сил притяжения от радиуса орбиты планеты в метрах.
Рис. 32. График зависимости отношения моментов сил притяжения от радиуса орбиты планеты в метрах.
Если верна теория то у Венеры, Земли и Марса родных спутников вообще быть не может, а у Нептуна должно быть больше всех родных спутников (самое большое отношение моментов сил притяжения). Но в системе Нептуна в прошлом произошла катастрофа и (почти) все родные спутники были утеряны. Для
Фаэтона с учётом его массы и массы тогдашней Луны расстояние между ними было около 19600 км, что делает систему Фаэтон-Луна настоящей кратной (если они не попадают в полости Роша друг друга). Теперь надо понять что значат коэффициенты в формуле аппроксимации.
Изучая данные по
Kepler-11 я обнаружил линейную зависимость параметра m/R
2 от параметра 1/a, где m-масса планеты, R-радиус планеты, a-радиус орбиты планеты. Эта зависимость выполняется для планет Kepler-10 и Kepler-9.
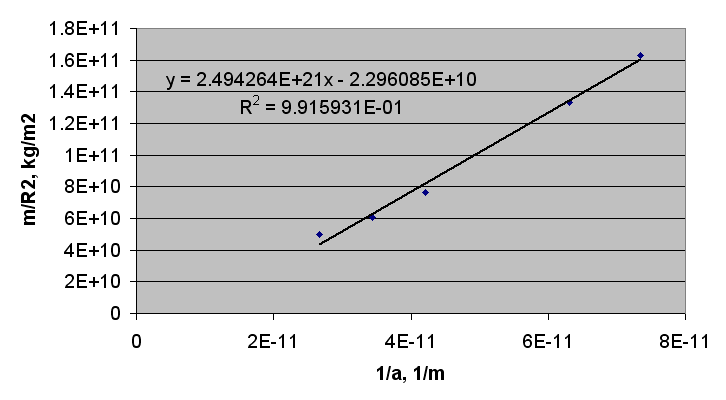 Рис. 33. График зависимости параметра m/R2 от параметра 1/a для планет системы Kepler-11.
Рис. 33. График зависимости параметра m/R2 от параметра 1/a для планет системы Kepler-11.
Масса второй (от звезды) планеты Kepler-11 с радиусом орбиты 0.106 а.е. была определена как 13.5+4.8/-6.1 масс Земли. С массой 13.5 масс Земли она сильно выбивается из линейной зависимости, но с массой 9 масс Земли (что в пределах погрешности) она располагается точно на прямой. В системе Kepler-10 вторая планета пока не подтверждена.
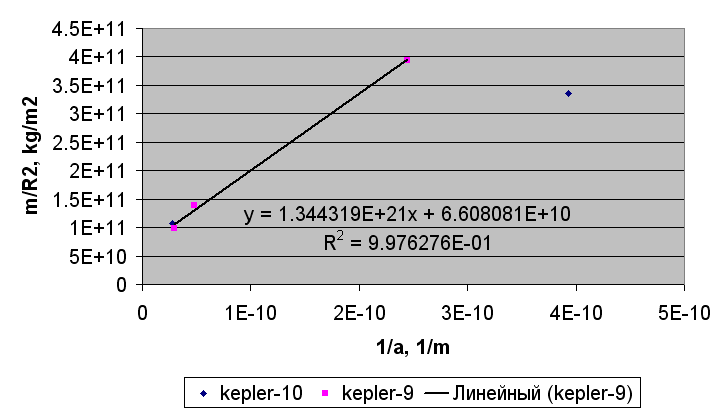 Рис. 34. График зависимости параметра m/R2 от параметра 1/a для планет систем Kepler-10 и Kepler-9.
Рис. 34. График зависимости параметра m/R2 от параметра 1/a для планет систем Kepler-10 и Kepler-9.
Для сферических (родных) спутников Юпитера эта зависимость выполняется без оговорок, для сферических спутников Сатурна и Урана эта зависимость выполняется с некоторыми оговорками - зависимость есть, но наклон прямой аппроксимации обратный.
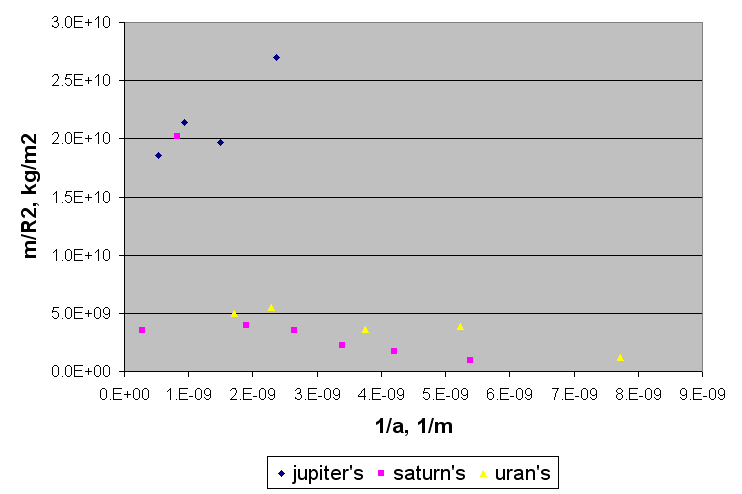 Рис. 35. График зависимости параметра m/R2 от параметра 1/a для спутников Юпитера, Сатурна и Урана.
Рис. 35. График зависимости параметра m/R2 от параметра 1/a для спутников Юпитера, Сатурна и Урана.
Для планет Солнечной системы зависимость выполняется для групп планет, отдельная зависимость для планет земной группы (Венера, Земля, Марс,
Фаэтон), отдельная зависимость для газовых гигантов (Юпитер, Сатурн, Уран, Нептун), отдельно для Меркурия.
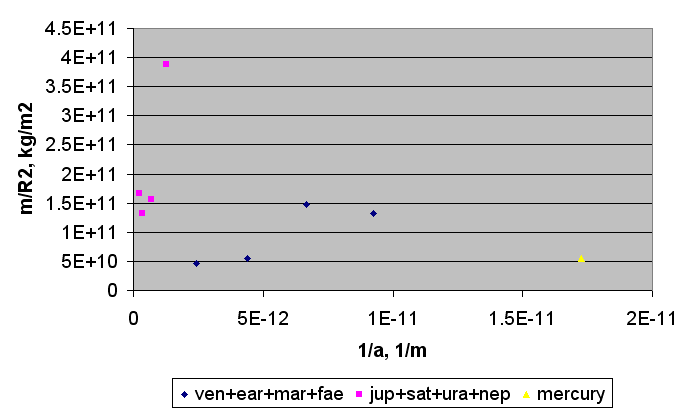 Рис. 36. График зависимости параметра m/R2 от параметра 1/a для планет Солнечной системы.
Рис. 36. График зависимости параметра m/R2 от параметра 1/a для планет Солнечной системы.
Эта зависимость выполняется для планет на малой параболе (проверено для звёзд с массой близкой к массе Солнца), и для спутников крупных планет с массой порядка массы Юпитера.
Зная формулу прямой аппроксимакции, можно по радиусу орбиты планеты определить параметр m/R
2. Радиусы орбиты планет определяем по алгоритму, описанному в пункте 3. Если по графику плотности планеты от радиуса орбиты можно определить предполагаемую плотность искомой планеты, то по плотности через m/R
2 можно найти радиус и массу планеты. Если известен радиус планеты, то из m/R
2 можно найти массу планеты. Если известна масса планеты то из m/R
2 можно найти радиус планеты.
В системе Kepler-11 по формуле прямой аппрокимации вычисляем параметр m/R
2 для последней (от звезды) планеты с радиусом орбиты 0.462 а.е., и, зная радиус, вычисляем массу планеты - 2.74 масс Земли. В этой системе три возможные планетные орбиты - планет на них пока не обнаружили, возможно это незанятые планетные орбиты, возможно планеты на этих орбитах есть, но слишком маломассивные. Но, если предположить их плотность, то можно рассчитать предположительные массу и радиус этих планет.
 Рис. 37. Планеты малой параболы системы Kepler-11.
Рис. 37. Планеты малой параболы системы Kepler-11.
Жёлтым цветом показано изменённое в пределах погрешности значение. Зелёным цветом показаны расчитанные значения.
В системе Kepler-9 между первой и второй планетами находятся три возможные планетные орбиты, на которых пока не обнаружили планет. Если предположить их плотности, то можно вычислить их предполагаемые массы и радиусы.
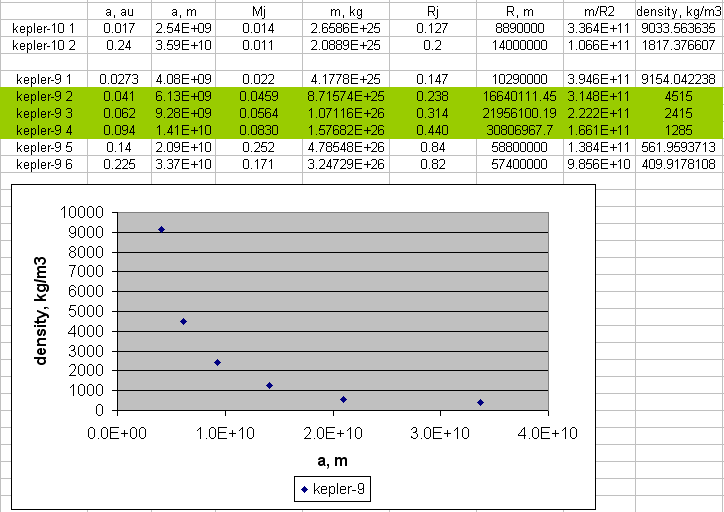 Рис. 38. Планеты малой параболы систем Kepler-9 и Kepler-10.
Рис. 38. Планеты малой параболы систем Kepler-9 и Kepler-10.
Зелёным цветом показаны расчитанные значения.
Не стоит считать предполагаемые плотности планет близкими к реальности. Дальнейшие исследования подтвердят или опровергнут зависимость параметра m/R
2 от параметра 1/a.
Дальнейшие исследования систем Kepler-9, Kepler-10 и Kepler-11 показали, что формула закономерности, выполняющейся для планет на малой параболе, очень сильно похожа на формулу закономерности в электромагнитных явлениях. Подробное изучение выявило, что при замене в формулах Максвелла электрического заряда на массу эти формулы подходят для описания состояния любых звёзд, планет и их спутников. Из уравнений Максвелла при замене электрического заряда на массу выводятся: уравнение зависимости массы от плотности, уравнение силы притяжения Ньютона, основное уравнение динамики вращательного движения твёрдого тела.
В электромагнетизме переменное электрическое поле порождает вихревое магнитное поле и переменное магнитное поле порождает вихревое электрическое поле. В гравитации переменное гравитационное поле порождает вихревое роторное поле и переменное роторное поле порождает вихревое гравитационное поле.
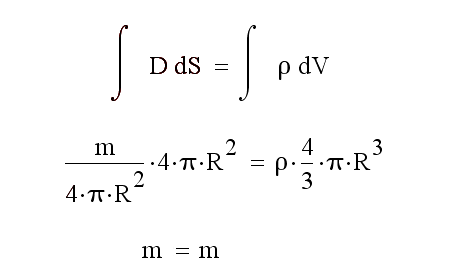 Рис. 39. Первое уравнение, связывающее гравитационную индукцию D с плотностью тела ρ.
Рис. 39. Первое уравнение, связывающее гравитационную индукцию D с плотностью тела ρ.
В этом уравнении D-гравитационная индукция тела, S-площадь поверхности тела, ρ-плотность тела, V-объём тела, R-радиус тела. Из этого уравнения следует, что масса тела равна произведению гравитационной индукции на площадь тела и равна произведению плотности тела на объём тела.
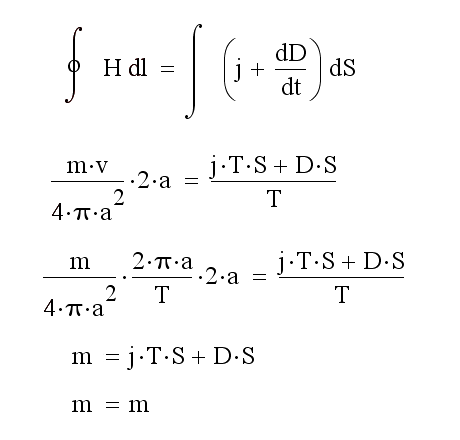 Рис. 40. Второе уравнение, связывающее напряжённость роторного поля H с гравитационной индукцией D.
Рис. 40. Второе уравнение, связывающее напряжённость роторного поля H с гравитационной индукцией D.
В этом уравнении H-напряжённость роторного поля движущегося тела, l-радиус орбиты тела, D-гравитационная индукция тела, S-площадь тела, T-период движения тела по орбите, j-плотность тока смещения массы тела, m-масса тела, v-скорость тела, a-радиус орбиты тела. Произведение напряжённости роторного поля тела на радиус орбиты тела равна массе тела и равна сумме плотностей тока смещения и тока проводимости массы тела, умноженной на площадь тела.
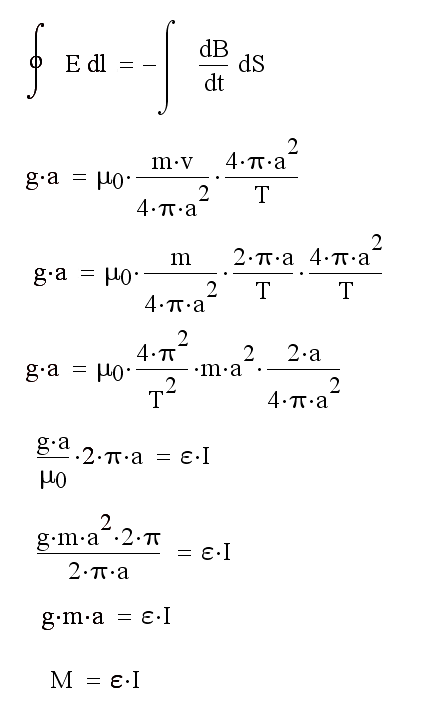 Рис. 41. Третье уравнение, связывающее напряжённость гравитационного поля E с индукцией роторного поля B.
Рис. 41. Третье уравнение, связывающее напряжённость гравитационного поля E с индукцией роторного поля B.
В этом уравнении E-напряжённость гравитационного поля тела, l-радиус орбиты тела, B-индукция роторного поля тела, T-период движения тела по орбите, S-площадь тела, m-масса тела, v-скорость тела, a-радиус орбиты тела, T-период движения тела по орбите, μ
0-роторная проницаемость пространства, ε-угловое ускорение тела. Произведение напряжённости гравитационного поля тела на радиу орбиты равно произведению индукции роторного поля тела на площадь тела, поделённых на период движения тела по орбите. Из этого уравнения выводится основное уравнение динамики вращательного движения твёрдого тела: M=ε*I, где M-момент силы, действующей на тело, ε-угловое ускорение тела, I-момент инерции тела. Из этого уравнения выводится уравнение Кеплера.
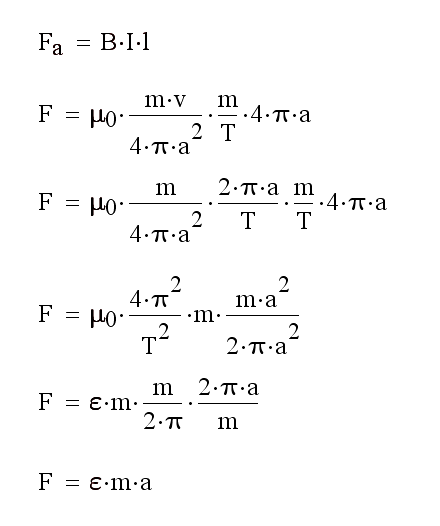 Рис. 42. Четвёртое уравнение, определяющее силу, действующую на тело.
Рис. 42. Четвёртое уравнение, определяющее силу, действующую на тело.
В этом уравнении F-сила, действующая на первое тело со стороны всех тел в системе, B-индукция роторного поля первого тела, I-сила тока массы первого тела, l-перемещение первого тела, m-масса первого тела, v-скорость первого тела, a-радиус орбиты первого тела, T-период движения первого тела по орбите, μ
0-роторная проницаемость пространства, ε-угловое ускорение первого тела. Произведение индукции роторного поля на силу тока массы тела и на перемещение равно силе, действующей на это тело со стороны всех других тел в системе. Из конечного уравнения выводится формула ньютоновской силы притяжения двух тел, если расписать угловое ускорение по формуле Кеплера.
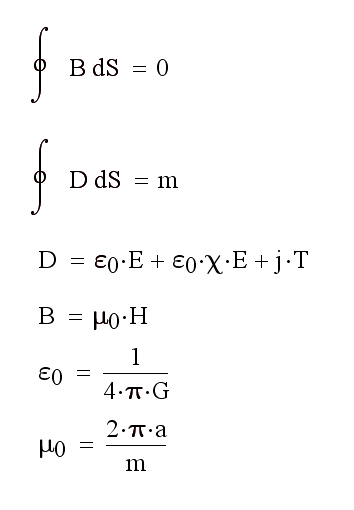 Рис. 43. Остальные уравнения гравироторных явлений.
Рис. 43. Остальные уравнения гравироторных явлений.
Первые два уравнения на рисунке 43 являются теоремой Гаусса для индукций гравитационного и роторного полей. Циркуляция вектора роторного поля по замкнутому контуру равна нулю, что значит отсутствие в природе роторных зарядов. Третье уравнение связывает гравитационную индукцию D с напряжённостью гравитационного поля E через гравитационную проницаемость пространства ε
0, гравитационную восприимчивость вещества χ и произведение плотности тока проводимости массы на период движения. Четвёртое уравнение связывает индукцию роторного поля B с напряжённостью роторного поля H через роторную проницаемость пространства μ
0. Последние два уравнения расписывают гравитационную и роторную проницаемости пространства.
Напряжённость гравитационного поля определяется как GM/a
2 и является ускорением свободного падения g, созданного телом на удалении a от него. Рассмотрим более подробно уравнение связи гравитационной индукции с напряжённостью гравитационного поля:
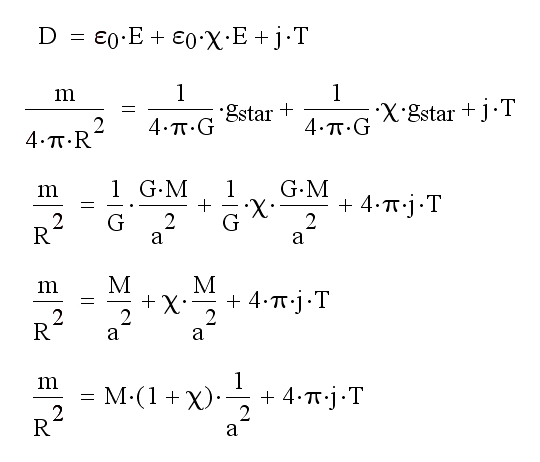 Рис. 44. Уравнение связи гравитационной индукции планеты с напряжённостью гравитационного поля звезды.
Рис. 44. Уравнение связи гравитационной индукции планеты с напряжённостью гравитационного поля звезды.
Это уравнение показывает зависимость гравитационной индукции планеты от напряжённости гравитационного поля звезды. Другими словами: ускорение свободного падения на поверхности планеты зависит от ускорения свободного падения звезды на орбите планеты. Именно эту зависимость Я обнаружил при изучении систем Kepler-9, Kepler-10 и Kepler-11, именно эта зависимость навела Меня на идею применимости уравнений Максвелла в гравитации. Уравнения зависимости гравитационной индукции планет от напряжённости гравитационного поля звезды для систем Kepler-9 и Kepler-11:
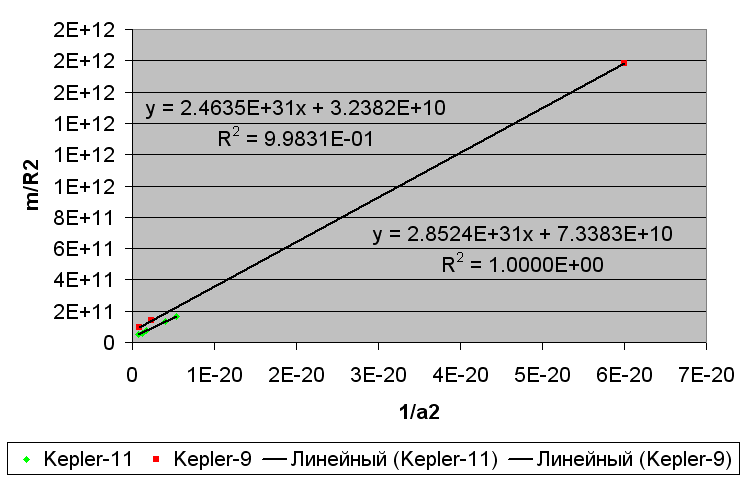 Рис. 45. Уравнения связи гравитационной индукции планет с напряжённостью гравитационного поля звезды в системах Kepler-9 и Kepler-11.
Рис. 45. Уравнения связи гравитационной индукции планет с напряжённостью гравитационного поля звезды в системах Kepler-9 и Kepler-11.
Поделим первые коэффиценты на массу звёзд и распишем уравнения через гравитационную восприимчивость вещества χ:
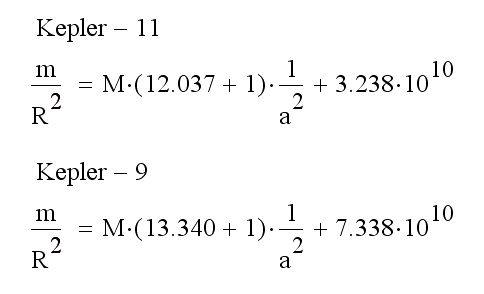 Рис. 45. Расписанные уравнения в системах Kepler-9 и Kepler-11.
Рис. 45. Расписанные уравнения в системах Kepler-9 и Kepler-11.
Из этих уравнений следует, что гравитационная восприимчивость вещества около звезды в системе Kepler-11 равна 12.037, а в системе Kepler-9 равна 13.340, разница между значениями небольшая. Гравитационная восприимчивость вещества характеризует вещество протопланетного диска, из которого сформировались планеты. Эти уравнения справедливы только для близких к звёздам планет, для планет на большой параболе коэффиценты уравнения будут другими.
Если рассматривать спутники планет, зависимость для которых показана на рисунке 35, то на спутники влияет как гравитационное поле планеты так и гравитационное поле звезды:
 Рис. 46. Уравнение связи гравитационной индукции спутника с напряжённостями гравитационного поля планеты и звезды.
Рис. 46. Уравнение связи гравитационной индукции спутника с напряжённостями гравитационного поля планеты и звезды.
При уменьшении расстояния от планеты до звезды сокращается максимальный радиус орбиты спутника вокруг планеты из-за увеличения напряжённости гравитационного поля звезды. Ближе некоторого расстояния до звезды у планет не формируются родные спутники. В солнечной системе предел формирования родных спутников находится между орбитами Марса и Цереры - от Цереры и дальше родные спутники у планет сформировались, а у Марса и ближе - нет.
Любое массивное тело, находясь в гравитационном поле другого тела, подвергается гравитационной поляризации. Поляризация возникает из-за того, что векторы напряжённости гравитационных полей двух тел между телами противонаправлены, а за любым (из этих двух) телом сонаправлены. Если рассмотреть планету, вращающуюся вокруг звезды, то на орбите планеты звезда создаёт напряжённость своего гравитационного поля, вектор которого направлен от планеты к звезде. Но планета создаёт напряжённость своего гравитационного поля, вектор которого направлен со всех сторон к центру планеты. На обращённой к звезде стороне планеты вектор собственной напряжённости гравитационного поля направлен от звезды и противонаправлен вектору напряжённости гравитационного поля звезды. На противоположенной стороне планеты вектор собственной напряжённости гравитационного поля направлен на звезду и сонаправлен с вектором напряжённости гравитационного поля звезды. На обращённом к звезде полушарии планеты ускорение свободного падения планеты уменьшается на величину ускорения свободного падения звезды на орбите планеты. На противоположенном от звезды полушарии планеты ускорение свободного падения планеты увеличивается на величину ускорения свободного падения звезды на орбите планеты. Разность величин напряжённости гравитационного поля ближнего и дальнего полушарий планеты и есть гравитационная поляризация планеты гравитационным полем звезды. Численно гравитационная поляризация равна удвоенному значению напряжённости гравитационного поля звезды на орбите планеты. Введём определение подзвёздной и противозвёздной точек. Подзвёздная точка - ближайшая к звезде точка на поверхности планеты, находится в центре обращённого к звезде полушария, векторы напряжённостей гравитационного поля планеты и звезды лежат на одной прямой и противонаправлены. Противозвёздная точка - наидальшая от звезды точка на поверхности планеты, находится в центре противоположенного звезде полушария, векторы напряжённости гравитационных полей планеты и звезды лежат на одной прямой и сонаправлены. В других точках на поверхности планеты векторы напряжённости гравитационного поля планеты и звезды не лежат на одной прямой и в зависимости от угла отклонения от оси подзвёздная точка - противозвёздная точка вектор напряжённости гравитационного поля звезды убывает на косинус этого угла. На перпендикулярном оси подзвёздная точка - противозвёздная точка меридиане планеты векторы напряжённости гравитационного поля планеты и звезды перпендикулярны друг другу.
Гравитационная поляризация создаёт гравитационный градиент на поверхности и в объёме планеты. Минимум градиента в подзвёздной точке, максимум в противозвёздной точке. Для близких к звезде планет гравитационная поляризация может быть очень большой, что отражается на форме планеты, её внутреннем строении и рельефе.
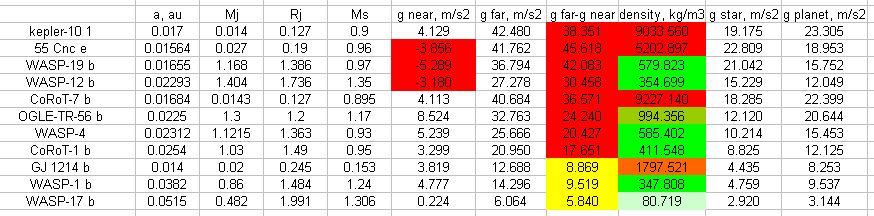 Рис. 47. Гравитационная поляризация некоторых горячих планет.
Рис. 47. Гравитационная поляризация некоторых горячих планет.
При сильной поляризации планета растягивается по оси, направленной на звезду. Вещество по бокам планеты смещается к минимуму градиента быстрее, чем вещество с полюсов. Поэтому длина полярной оси будет больше длины боковой оси планеты. Планета по форме будет похожа на вытянутый эллипсоид, сплющенный с боков. Такую форму имеет спутник Юпитера в Солнечной системе Амальтея.
Все горячие планеты поляризованы. У трёх планет напряжённость гравитационного поля в подзвёздной точке оказалась меньше нуля. Это планеты 55 Cnc e, WASP-19 b и WASP-12 b. Эти планеты вошли в полость Роша своих звёзд, теряют массу и разрушаются, как разрушаются спутники в Солнечной системе Ио и Энцелад. При большом градиенте напряжённости гравитационного поля на планете ядро будет смещаться к минимуму градиента, что будет разогревать планету. Вещество коры будет перетекать к минимуму градиента. Планета будет постепенно смещаться к звезде и в итоге будет разорвана приливными силами звезды. Возможен вариант, при котором планета по мере разогрева и приближения к звезде сбросит в космос всё вещество с низкой плотностью, останется только однородное по плотности ядро, которому будет некуда смещаться, в итоге орбита планеты стабилизируется. Скорее всего этот сценарий произошёл для планет CoRoT-7 b и Kepler-10 1. Именно из-за однородности внутреннего строения спутники Солнечной системы Мимас и Амальтея при высокой гравитационной поляризации не разрушаются и не смещаются.
© Lex Yakovenko, 2008-2011. All right reserved.